PROMETHEUS Lab

About Us

Welcome to the Probabilistic Methods for Estimation of Uncertain Systems (PROMETHEUS) Laboratory!

The PROMETHEUS Lab conducts research to solve complex and challenging problems in estimation, with specific emphasis in space domain awareness and spacecraft navigation. We develop novel theoretical and computational methods that address problems in nonlinear, non-Gaussian uncertainty propagation; Bayesian and non-Bayesian inference; conjunction assessment and collision avoidance; data association; multitarget tracking; vision-based navigation; terrain relative navigation; extended object tracking; and attitude dynamics, determination, and control.

Below, you will find descriptions of some of the recent research projects being worked on by the PROMETHEUS Laboratory.

 

 

 

 

 

 

 

 

 

 

 


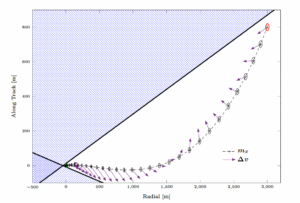
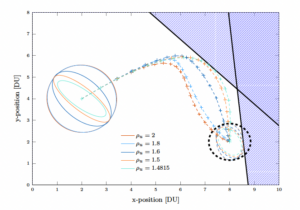
A future with thousands of spacecraft operating in cislunar space requires autonomous guidance and navigation. A key challenge in autonomy is ensuring reliability in the face of uncertainties. These assets must reliably perform their intended functions despite a lack of certainty in the position and velocity of the object, environmental disturbances, and system parameters. This line of research focuses on optimizing the paths of spacecraft without assuming perfect knowledge of the spacecraft’s position and speed.

This capability exists for Earth-based satellites, but it requires computers on the ground to churn through thousands of simulations to verify that the optimized path is indeed a reliable one. Our research seeks to eliminate the need for ground-based verification by designing optimization schemes that inherently return reliable paths for the spacecraft — and designing them in a way that is amenable to onboard use.

Much of modern spacecraft navigation relies on linear estimation techniques, most notably the Kalman filter and its various extensions and adaptations; however, to enable future, more ambitious and scientifically fruitful space exportation, advancements in navigation, orbit determination, and onboard dynamic state estimation are required. This research develops novel techniques for nonlinear filtering and robust statistical inference. The former seeks to maximally utilize the limited information and measurement capabilities inherent in space exploration, while the latter ensures any such estimator remains cognizant and resilient of the inconsistencies between one’s idealized physical models and the true dynamical environment.

Conventional approaches to nonlinear estimation require computational capabilities far exceeding modern flight computers and, in some instances, even ground-based networks. To that end, this research proposes novel, homotopic methods that demonstrates improved performance over the Kalman filter and its derivatives while remaining computationally feasible for real-time navigation, with numerical costs comparable to the prediction stage of a Kalman filter. Homotopic filters operate by defining a smooth mapping from the prior to the posterior estimate in the form of a first-order, ordinary differential equation (ODE). This ODE may then be integrated over a finite domain, providing updates to the state estimate and its associated covariance or, for ground-based orbit determination with more computational resources, updates to particle ensemble or Gaussian mixture representations of state uncertainty.

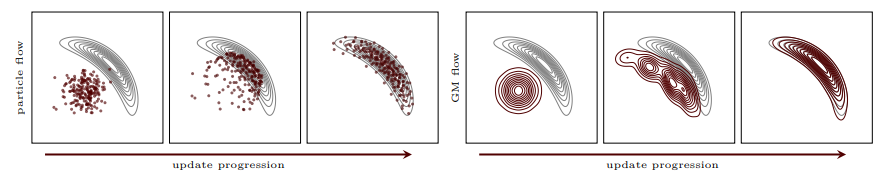
Homotopic filtering also allows many of the limiting assumptions in Kalman filtering to be relaxed, e.g., additive white noise or Euclidean measurements, accommodating a wider breadth of measurement models for which the Kalman filter is ill-suited or, in extreme circumstances, undefined. In so doing, homotopic filtering also permits robust modifications to traditional techniques in linear estimation and Bayesian inference, accommodating more robust update policies, such as those using heavy-tailed distributions, mitigating the influence of outliers and modeling errors without requiring ad hoc modifications to the underlying update, e.g., measurement editing and underweighting.

This work leverages advanced filtering methods, particularly the fusion (also known as inverse) extended Kalman filter (FEKF), to enable highly precise state estimation and adaptive sensing in the challenging environment of cislunar space. The FEKF approach models complex, nonlinear dynamics that are typical in space exploration, facilitating real-time adjustments to navigation and sensor inputs. The resulting algorithms enable applications including threat detection (or classification) and active sensing for cislunar navigation and control.

The FEKF is comprised of two phases: the alpha and the omega filters. The alpha filter is a standard EKF, while the omega filter is given the task to find a more accurate alpha filter’s estimate based on its state transition equations. Monte Carlo simulations are used to test these filters under changing initial conditions; conclusions about the accuracy and statistical consistency are obtained from these experiments. The time-averaged mean square error (AMSE) is also used as a measure to indicate the performance of the omega filter over the alpha filter’s AMSE, showing that the overall omega AMSE is significantly lower than that of the original filter.

A general solution to estimation problems is given by Bayes’ rule, and, for systems with unconstrained states, a multitude of approximations of varying fidelity and computational complexity have been developed. It is, however, common for estimation problems to involve some constraints on the states of the uncertain system. One example that’s very common in spacecraft navigation is the attitude quaternion—a unit vector on the four-dimensional unit sphere. Other possible examples of constrained states are the classical orbital elements or the parameters of an inertia tensor. These constraints are often ignored or handled in an ad hoc manner to shoehorn the problem into an unconstrained estimation approach. This is exactly the situation for recursive attitude estimation where the usual approach is to approximate deviations from the estimated attitude as unconstrained vector quantities then apply an unconstrained estimator, such as the extended Kalman filter. This approach tends to be effective for small attitude uncertainty but falls apart for larger uncertainty.

This research investigates ways to design estimators that work on the same manifold as the system states to solve the problem of constrained estimation. These methods can be applied to enforce inequality constraints when estimating inertia tensor parameters. The approaches are also extended to the problem of attitude estimation using directional statistics (probability distributions defined on the unit circle, the unit sphere, or spheres of higher dimensions) to design estimators for angular states that directly account for inherent constraints. Appropriately accounting for these kinds of state constraints facilitates the development and deployment of more accurate and robust filters for constrained problems such as those that frequently arise in navigation and space object tracking.


As space domain awareness architectures expand, there is a growing need to perform higher fidelity space object tracking, particularly when spacecraft perform maneuvers. While modern estimation techniques are capable of tracking orbiting targets, these methods often struggle to capture objects that maneuver. When a space vehicle maneuvers, the characteristics of its motion are difficult to capture due to the coupled nature of the time, magnitude, and direction of the maneuver. To develop a maneuver estimation framework, the hybrid Bernoulli filter was selected and utilized using assumptions on the magnitude and direction of the maneuver.

Our research focuses on developing multiple hypothesis methods to represent spacecraft maneuvers by incorporating multiple modes of the potential dynamics of the vehicle. By forming hypotheses of motion based on combinations of these modes, our method can track objects through switching dynamics (i.e., thrusters turning on and off). Comparing received measurements to the enumerated hypotheses enables the tracking architecture to select the most likely hypothesis and estimate the maneuver profile. Our approach facilitates both impulsive and low thrust maneuvers, and recent developments have focused on incorporating maneuver magnitude uncertainty within the filter and tracking through large measurement gaps.